小升初数学暑假《求阴影部分面积》提高必练
-
简介
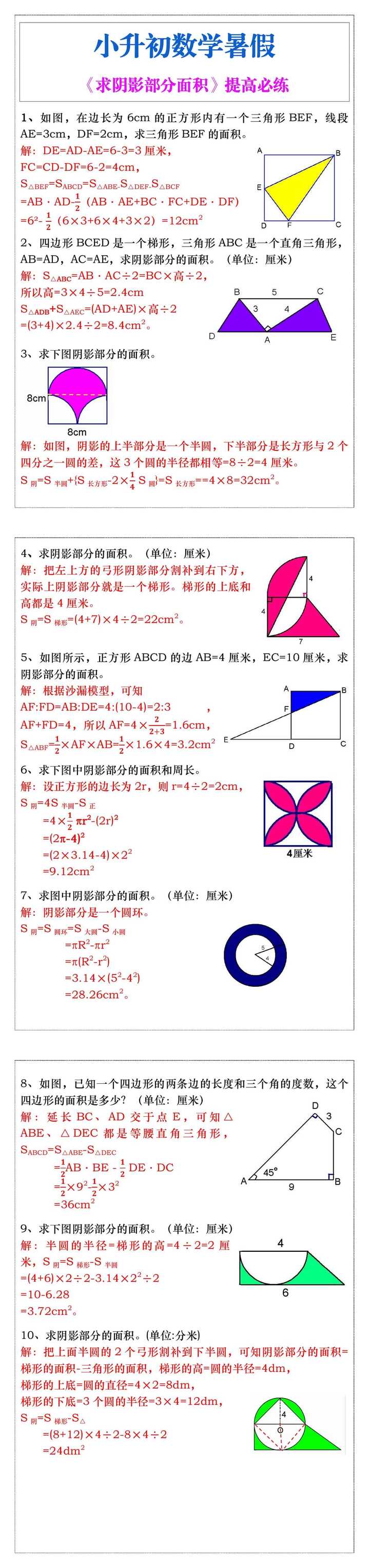
1、如图,在边长为6cm的正方形内有一个三角形BEF,线段AE=3cm,DF=2cm,求三角形BEF的面积。 解:DE=AD-AE=6-3=3厘米, FC=CD-DF=6-2=4cm, S△BEF=SABCD=S△ABE-S△DEF-S△BCF =AB·AD-(AB·AE+BC·FC+DE·DF) =6²- (6×3+6×4+3×2)=12cm2 2、四边形BCED是一个梯形,三角形ABC是一个直角三角形,AB=AD,AC=AE,求阴影部分的面积。(单位:厘米) 解:S△ABC=AB·AC÷2=BC×高÷2, 所以高=3×4÷5=2.4cm S△ADB+S△AEC=(AD+AE)×高÷2 =(3+4)×2.4÷2=8.4cm2。 3、求下图阴影部分的面积。 解:如图,阴影的上半部分是一个半圆,下半部分是长方形与2个四分之一圆的差,这3个圆的半径都相等=8÷2=4厘米。 S阴=S半圆+{S长方形-2× S圆}=S长方形==4×8=32cm2。
本年级热门下载
同类热门下载