小学数学【几何图形的九大解法】例题解析
-
简介
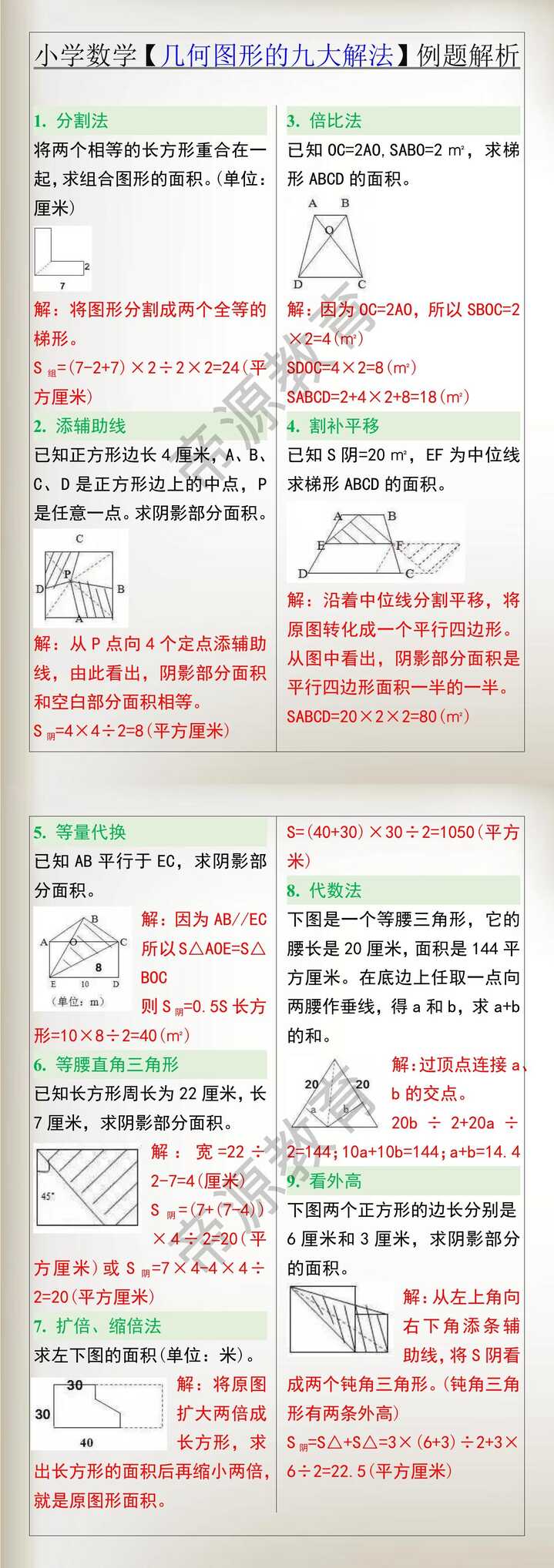
1.分割法 将两个相等的长方形重合在一起,求组合图形的面积。(单位:厘米) 解:将图形分割成两个全等的梯形。 S组=(7-2+7)×2÷2×2=24(平方厘米) 2.添辅助线 已知正方形边长4厘米,A、B、C、D是正方形边上的中点,P是任意一点。求阴影部分面积。 解:从P点向4个定点添辅助线,由此看出,阴影部分面积和空白部分面积相等。 S阴=4×4÷2=8(平方厘米) 3.倍比法 已知OC=2AO,SABO=2㎡,求梯形ABCD的面积。 解:因为OC=2AO,所以SBOC=2×2=4(㎡) SDOC=4×2=8(㎡) SABCD=2+4×2+8=18(㎡) 4.割补平移 已知S阴=20㎡,EF为中位线求梯形ABCD的面积。 解:沿着中位线分割平移,将原图转化成一个平行四边形。从图中看出,阴影部分面积是平行四边形面积一半的一半。 SABCD=20×2×2=80(㎡)
本年级热门下载
同类热门下载